Uncertain or Inadmissible numerical or time-date values
Both Uncertain numerical values
and Inadmissible numerical values, as
well as Uncertain time-date values
and Inadmissible time-date values,
can be calculated using con_limit_deviations).
When specifying limits = "SOFT_LIMITS" the check does not
identify inadmissible but uncertain values, according to the specified
ranges. An example call is:
# Load dataquieR
library(dataquieR)
# Load data
sd1 <- prep_get_data_frame("ship")
# Load metadata
prep_load_workbook_like_file("ship_meta_v2")
meta_data_item <- prep_get_data_frame("item_level") # item_level is a sheet in ship_meta_v2.xlsx
# Apply indicator function
MyValueLimits <- con_limit_deviations(
study_data = sd1,
meta_data = meta_data_item,
label_col = "LABEL",
limits = "HARD_LIMITS"
)A table output provides the number and percentage of all the range violations for the variables specifying limits in the metadata:
MyValueLimits$SummaryData| Variables | Limits | Below.limits-N (%) | Within.limits-N (%) | Above.limits-N (%) | |
|---|---|---|---|---|---|
| 1 | DBP_0.2 | HARD_LIMITS | 0 (0) | 2148 (100) | 0 (0) |
| 4 | DBP_0.2 | DETECTION_LIMITS | 0 (0) | 2148 (100) | 0 (0) |
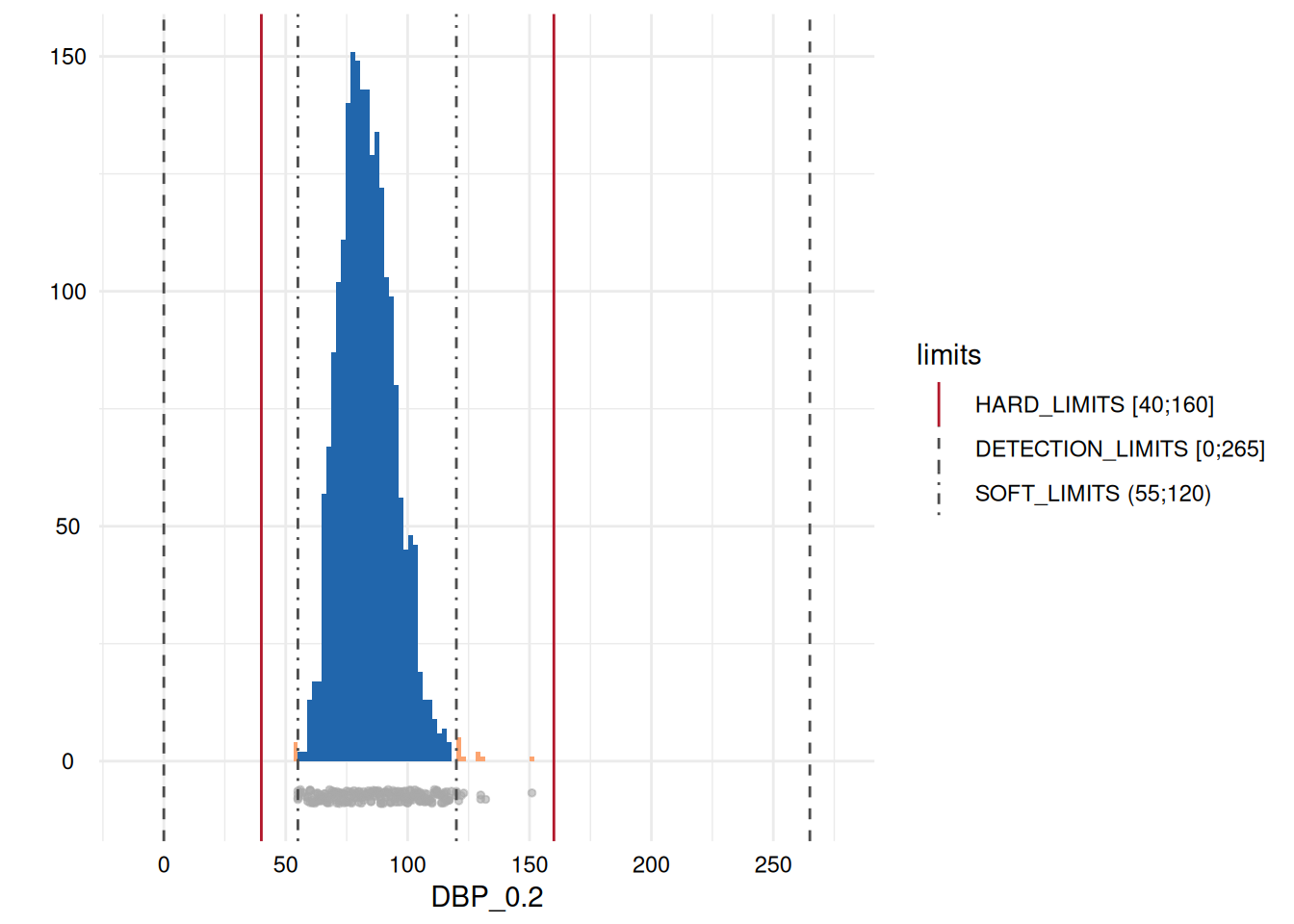
| 7 | DBP_0.2 | SOFT_LIMITS | 4 (0.19) | 2134 (99.35) | 10 (0.47) |
| 10 | BODY_HEIGHT_0 | HARD_LIMITS | 0 (0) | 2151 (100) | 0 (0) |
| 13 | BODY_WEIGHT_0 | HARD_LIMITS | 0 (0) | 2150 (100) | 0 (0) |
| 16 | WAIST_CIRC_0 | HARD_LIMITS | 0 (0) | 2148 (100) | 0 (0) |
| 19 | EXAM_DT_0 | HARD_LIMITS | 0 (0) | 2154 (100) | 0 (0) |
| 22 | CHOLES_HDL_0 | HARD_LIMITS | 0 (0) | 2138 (100) | 0 (0) |
| 25 | CHOLES_LDL_0 | HARD_LIMITS | 0 (0) | 2126 (100) | 0 (0) |
| 28 | CHOLES_ALL_0 | HARD_LIMITS | 0 (0) | 2139 (100) | 0 (0) |
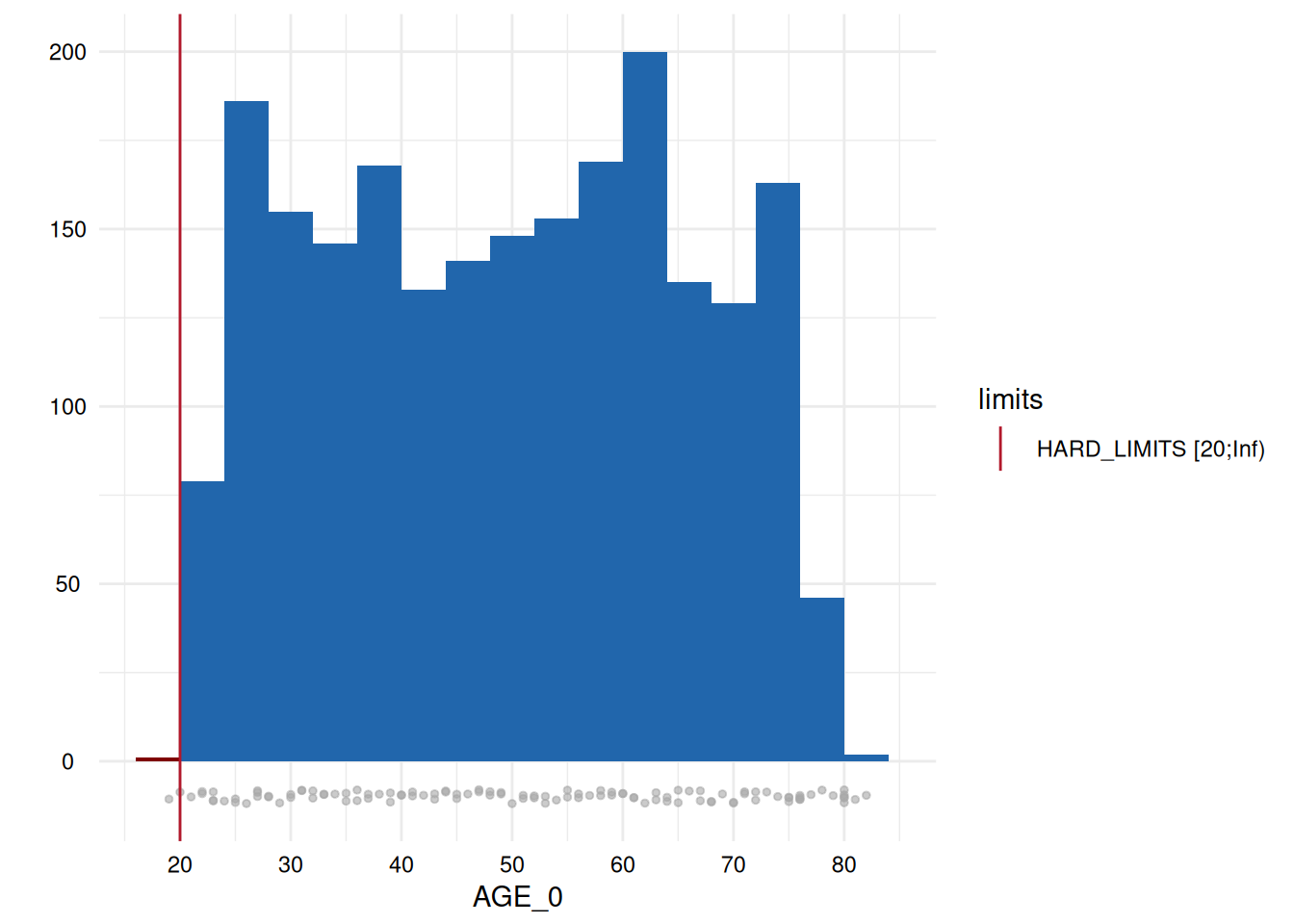
| 31 | AGE_0 | HARD_LIMITS | 1 (0.05) | 2153 (99.95) | 0 (0) |
| 34 | SBP_0.1 | HARD_LIMITS | 0 (0) | 2131 (99.02) | 21 (0.98) |
| 37 | SBP_0.1 | DETECTION_LIMITS | 0 (0) | 2131 (100) | 0 (0) |
| 40 | SBP_0.1 | SOFT_LIMITS | 4 (0.19) | 2031 (95.31) | 96 (4.5) |
| 43 | SBP_0.2 | HARD_LIMITS | 0 (0) | 2134 (99.35) | 14 (0.65) |
| 46 | SBP_0.2 | DETECTION_LIMITS | 0 (0) | 2134 (100) | 0 (0) |
| 49 | SBP_0.2 | SOFT_LIMITS | 4 (0.19) | 2071 (97.05) | 59 (2.76) |
| 52 | DBP_0.1 | HARD_LIMITS | 0 (0) | 2150 (99.91) | 2 (0.09) |
| 55 | DBP_0.1 | DETECTION_LIMITS | 0 (0) | 2150 (100) | 0 (0) |
| 58 | DBP_0.1 | SOFT_LIMITS | 2 (0.09) | 2139 (99.49) | 9 (0.42) |
The last column of the table also provides a GRADING. If the
percentage of violations is above some threshold, a GRADING of 1 is
assigned. In this case, any occurrence is classified as problematic.
Otherwise, the GRADING is 0.
The following statement assigns all variables identified as
problematic to an object whichdeviate to enable a more
targeted output, for example, to plot the distributions for any variable
with violations along the specified limits:
# select variables with deviations
whichdeviate <- as.character(
MyValueLimits$SummaryTable$Variables)[
MyValueLimits$SummaryTable$FLG_con_rvv_unum == 1 |
MyValueLimits$SummaryTable$FLG_con_rvv_utdat == 1 |
MyValueLimits$SummaryTable$FLG_con_rvv_inum == 1 |
MyValueLimits$SummaryTable$FLG_con_rvv_itdat == 1 ]
whichdeviate <- whichdeviate[!is.na(whichdeviate)]We can restrict the plots to those where variables have limit
deviations, i.e., those with a GRADING of 1 in the table above, using
MyValueLimits$SummaryPlotList[whichdeviate] (only the first
two are displayed below to reduce file size):
